20.05.2014
После того, как успешно получилось нарисовать строчку “да!” следующим шагом стало включение отрисовки шрифтов в конвейер. Причем задачу я поставил такую, чтобы отрисовка 2D (в экранных координатах) и 3D (в мировых) выполнялось как можно более идентичным кодом, а еще лучше – одним и тем же с парой настроек. Пришлось немного доработать конвейер и реализовать таки 2D камеру (до этого была только 3d, а 2d интерфейс рисовался с помощью пары хаков в рендере). Но в итоге результат превзошел все ожидания. Шейдеры (и пиксельный, и вершинный) – абсолютно одни и те же. Код объекта отрисовки (render entry) практически одинаковый, с одной лишь выборкой – брать матрицу проекции-вида из 2d или 3d камеры. Кроме того, благодаря такому объединению практически бесплатно получился еще и billboarding.
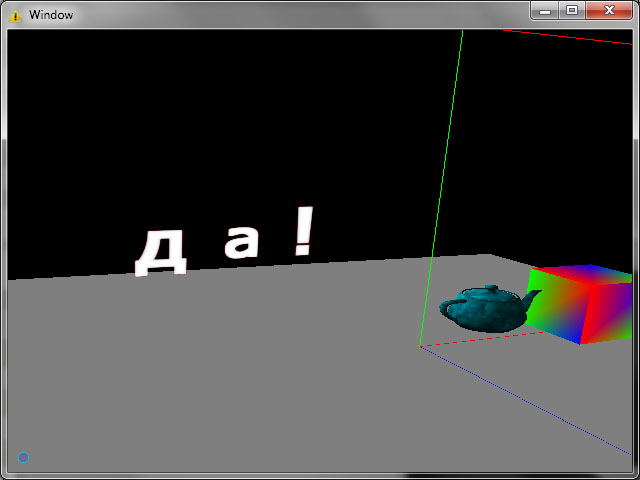
А теперь картинки, в нижнем углу маленькими буквами “да!” в экранных координатах. Справа – “да!” в мировых координатах, слева – “да!” в мировых координатах с применением технологии billboarding. Биллбоард однозначно видно по мере смещения и поворота камеры.
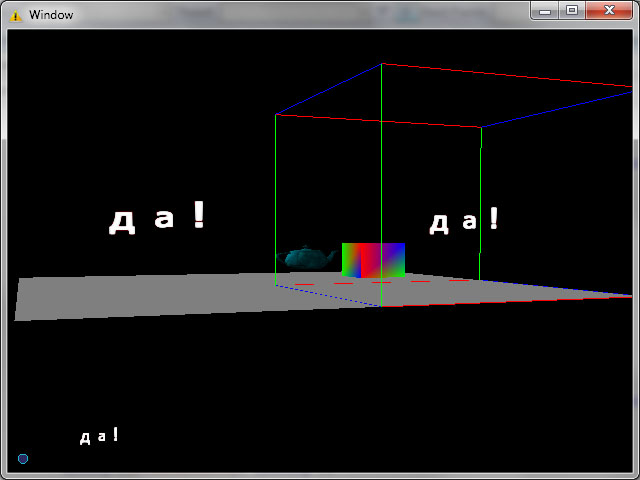
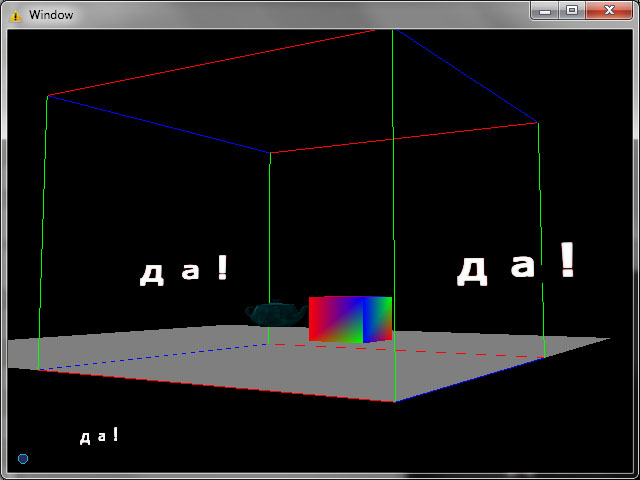
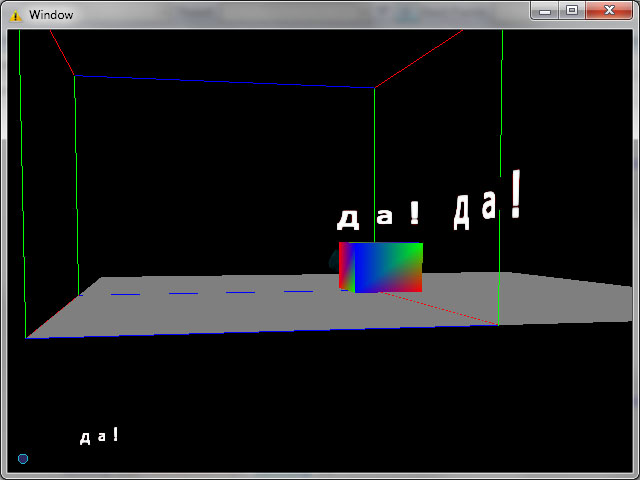
P.S. К слову, полученные алгоритмы и шейдеры впоследствии пригодятся когда буду реализовывать системы частиц (Particle Systems)
14.05.2014
Просто сказать, но не так просто сделать. В ходе попыток сделать вывод строк, обнаружилось, что во-первых, не все нужные параметры выгружались, во-вторых, центрирование букв в текстуре привело к забавным эффектам (один только восклицательный знак толщиной в три пикселя чего стоит), в-третьих, расчет текстурных координат для шейдера надо проводить с учетом форматного соотношения сторон буквы, а не просто по краю канвы.
Но все проблемы были таки решены и сегодня показываю рендер строчек, пока рисуем только “да!”, отчасти от того, что конвейер движка еще не совсем готов рисовать буквы шейдерами, но я двигаюсь в этом направлении. Как только появится возможность рендерить строчки любые, нарисую что-нибудь посложнее и по длиннее. Пока же, только “да!”.
Кстати, выяснилось, что придется реализовывать traits для STL’евской basic_string чтобы она могла поддерживать правильно мой тип unichar (typedef unsigned long). Но об этом в другой раз.
И еще, то что буквы рисуются в “мировых” координатах – это я так захотел. При желании можно сделать так чтоб строки стали биллбордами, или же рисовать в экранных координатах. Все зависит только от матрицы проекции-вида. Здесь она для мира.
А теперь обещанные рендеры:
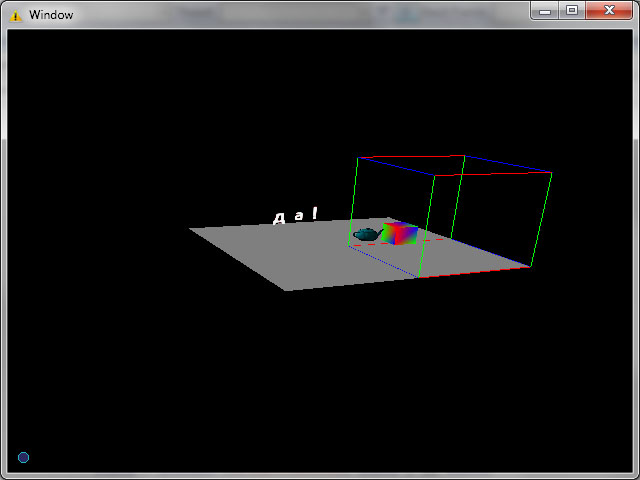

03.05.2014
После того, как удалось нарисовать букву “g”, следующим логичным шагом было бы нарисовать буквы русские, т.е. Юникод. Однако возникает одна небольшая проблема. Имя ей – UTF-8, а точнее – отсутствие встроенных в С++ нормальных механизмов работы с unicode (wchar_t не в счет – это не совсем Юникод). Пока для целей тестирования были взяты определенные коды символов (буквы ё и ѣ), получены их utf-8 коды (0xd1 0×91 и 0xd1 0xa3 соответственно) и уже по этим кодам рассчитаны необходимые данные.
В дальнейшем же при визуализации текста стоит решить, какого подхода придерживаться. Можно использовать UTF-8 и const char, либо wchar_t. Первый вариант дает более компактное представление, но функции strcmp, strlen и т.д. будут работать неправильно. С точки же зрения wchar_t функции будут работать правильно, но в Windows sizeof(wchar_t) = 2, что не совсем Юникод, и кроме того, например, китайские символы – это три байта даже в UTF-8. Поэтому хочется const char и UTF-8, посмотрим что получится.
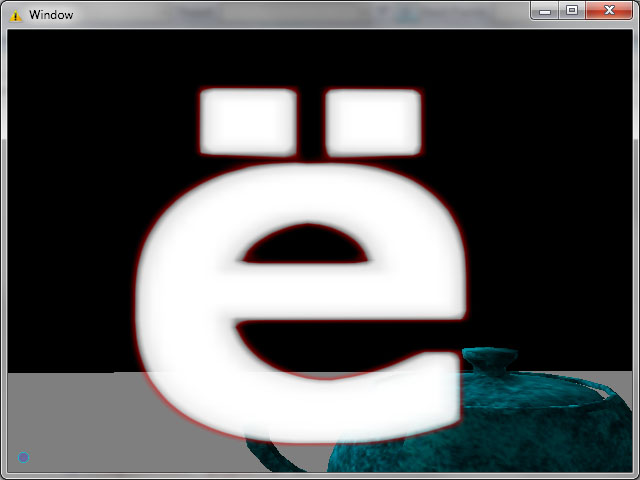
А теперь что получилось, буквы взяты специально экзотические
“ё”
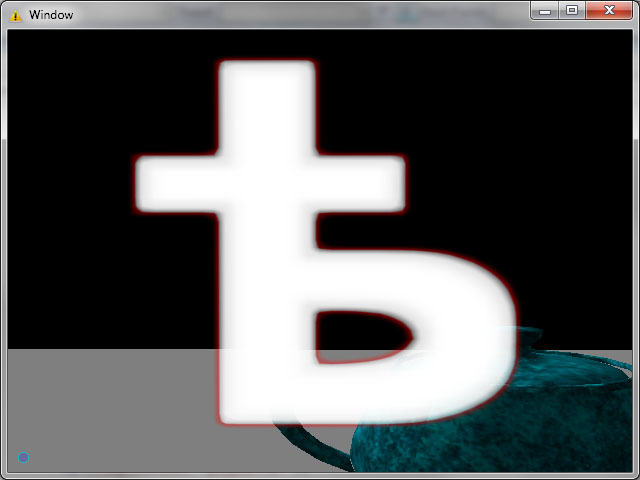
“ѣ” (ять, да-да тот самый ять :) )
30.04.2014
У меня таки получилось победить артефакты в рендерах, которые я приводил раньше. Однако это потребовало вычисления в шейдере факта попадания точки в контур глифа. Все это привело к ужасающему падению производительности. Т.к. все кривые глифа задавались аналитически и шейдеру приходилось все это рассчитывать в реальном времени.
В качестве оптимизации можно было бы конечно один раз глиф отрисовать в рендер-таргет, а потом просто блит, но это равносильно предрасчету глифов и просто блиту, разве что не во время разработки, а при старте.
Поэтому аналитическую информацию решено было предрасчитать и “запечь” в текстуру, а потом ей только пользоваться. С учетом фильтрации текстур еще и практически бесплатная интерполяция. С помощью библиотечки Cairo удалось просчитать нужную аналитическую информацию и быренько наваять шейдер. Вот что получилось.
Буква “g” при разных приближениях:
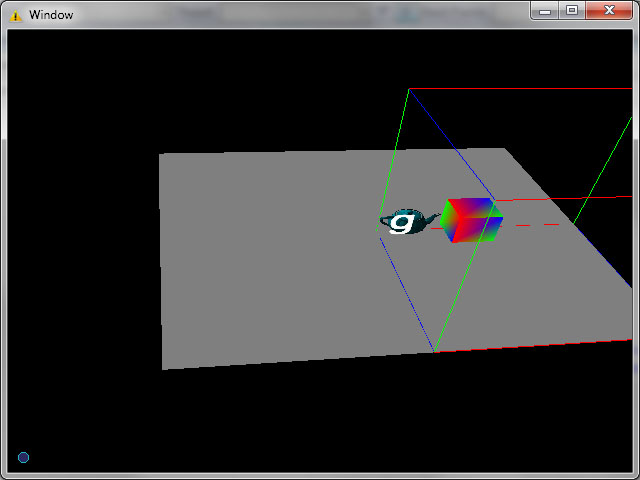
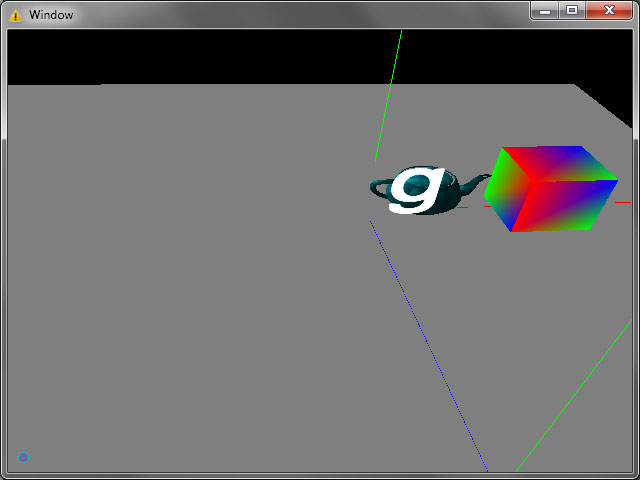
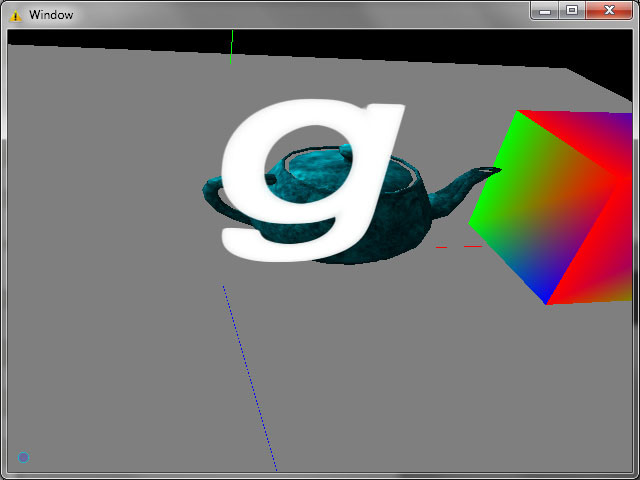

Как видно контуры плавные даже при огромном увеличении. Задача минимум (а изначально это вообще была задача максимум) достигнуто. Но дальше, как говориться, “Остапа понесло”.
Контур (красный), кроме того еще и плавный:

Тень (синяя), тоже плавная:
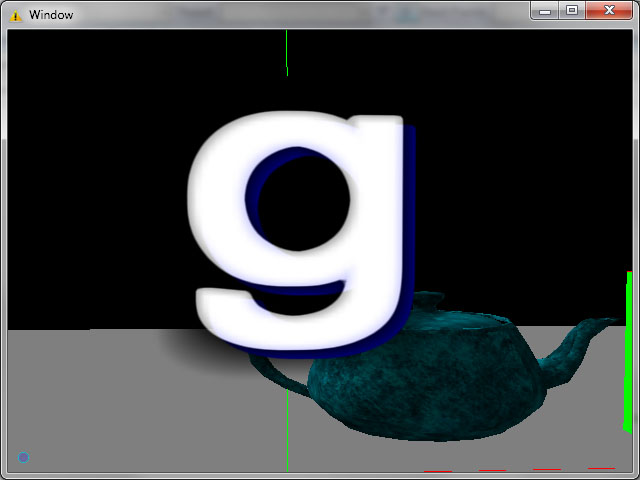
В принципе и тень и контур можно делать жесткими. Но плавными они эффектнее смотряться.
Ну и как обычно – чайник для антуража, плюс в этот раз еще и цветной куб. Так – эксперименты…
29.04.2014
Небольшая заметка. Может сэкономить кому-нибудь кучу времени. Понадобилось тут воспользоваться библиотекой Cairo, да еще чтоб png-шки с прозрачностью генерировать. Так вот, библиотека Cairo позволяет в формате ARGB32 использовать альфу, но только когда вы устанавливаете пиксель, то его нужно умножить на альфу. Иначе не получается.
Т.е. 50% красного будет выглядеть как 0×80800000 а не привычные 0x80ff0000















